Modelado de vigas mixtas Diamonds 2019

Este ejemplo extraído del Curso Cálculo de Estructuras con Diamonds, pretende mostrar una aproximación para modelizar vigas mixtas para cada una de las hipótesis de interacción entre elementos. Es decir, interacción completa, perfecta o parcial. Los modelos numéricos presentados se realizaron con el software Diamonds 2019.
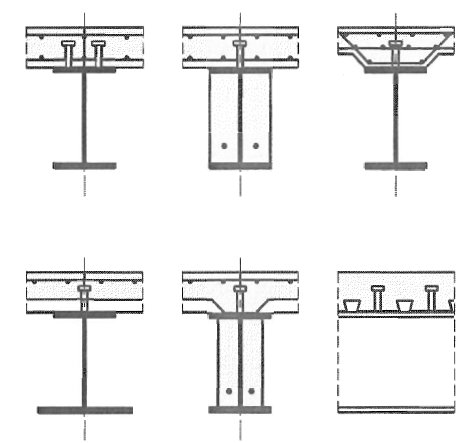
Figura 1. Viga mixta con conectores de cortante, extraída de EN 1994_1_1
Estas vigas pueden o no tener conectores de cortante. Dependiendo de los conectores utilizados, el comportamiento de estas puede ser de tres tipos:
| Sin interacción | Con interacción completa | Con interacción parcial |
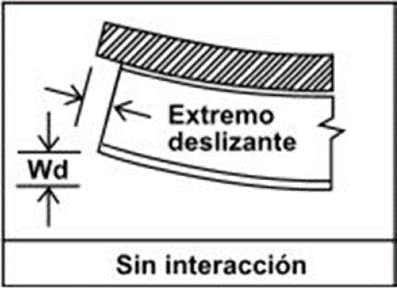
| La losa está apoyada sobre la viga de acero, y no existe adherencia entre ellas. En este caso no hay esfuerzo rasante y la losa desliza respecto a la viga. |
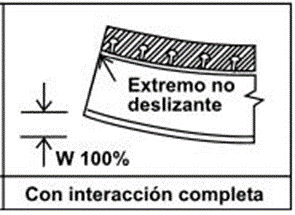
La losa de hormigón está perfectamente adherida a la viga de acero. En este caso ambos elementos trabajan solidariamente. |
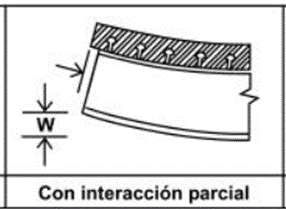
La losa de hormigón está imperfectamente adherida a la viga de acero. En este caso existe un grado de desplazamiento relativo entre la losa y la viga. |
|
|
|
Figura 2. Viga mixta sin interacción. |
Figura 3. Viga mixta con interacción perfecta. |
Figura 4. Viga mixta con interacción parcial. |
A continuación, se presentan tres modelos que representan estos distintos comportamientos. Además, se presenta una comparación con los resultados teóricos de desplazamiento de las vigas mixtas. Los modelos se hicieron con el software Diamonds 2019.
Para el ejemplo se consideró una viga mixta con las siguientes características:
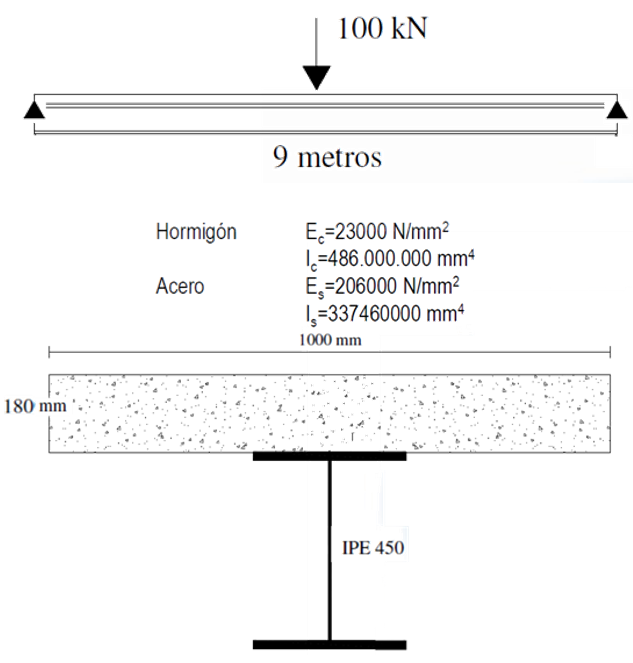
Figura 5. Datos y propiedades del ejemplo.
CASO 1: SIN INTERACCIÓN
RESULTADO EN DIAMONDS
Para modelizar este caso, primero se definen ambos elementos por separado. Se debe especificar que la parte superior de la viga coincida con la parte inferior de la losa.
Luego, se libera la transferencia de momento y cortante de la losa a la viga. De esta forma solo se transmiten esfuerzos axiles de un elemento a otro.
Según el programa, la máxima flecha de la viga en este caso es de 18 [mm].
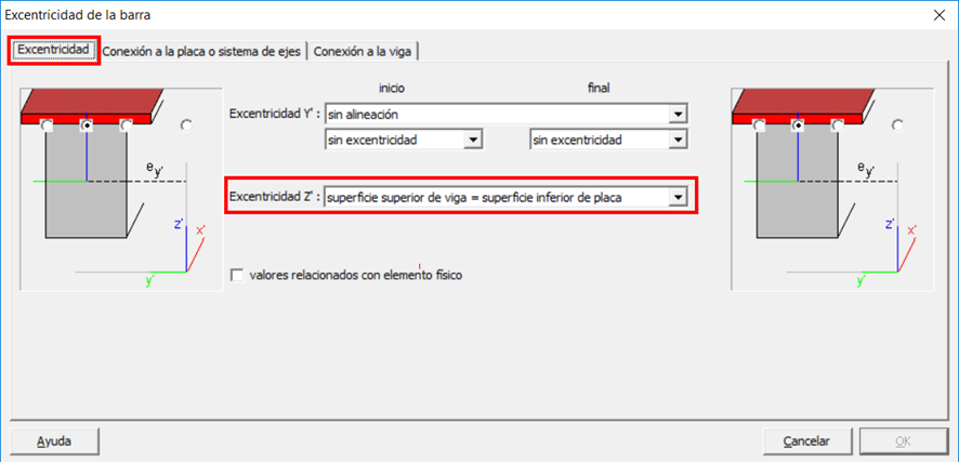
Figura 6. Punto de conexión entre ambos elementos.
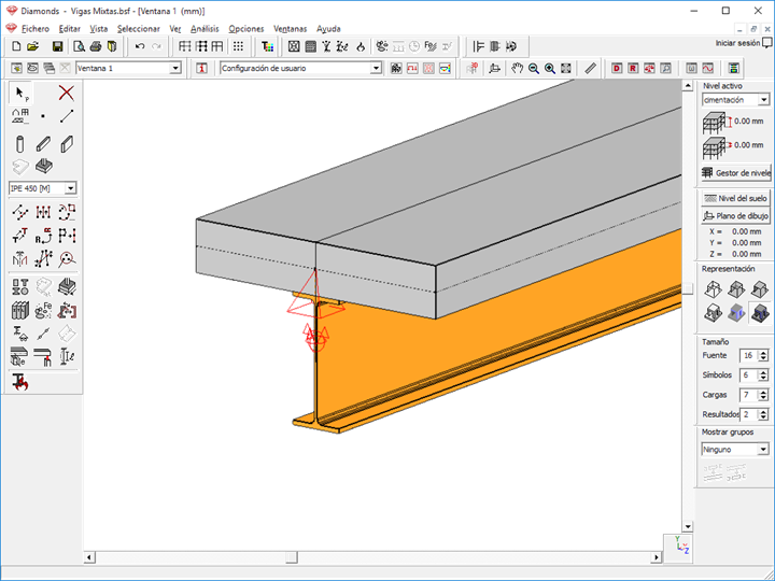
Figura 7. Modelo Diamonds Caso 1.
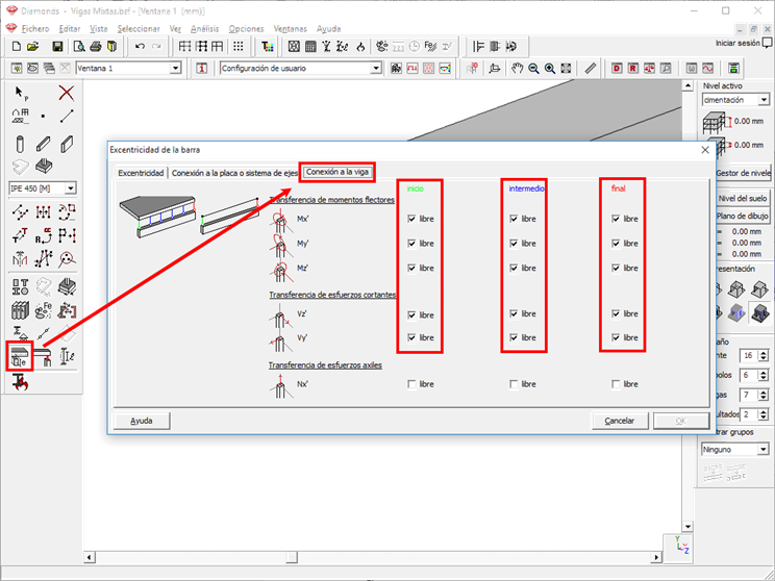
Figura 8. Interacción viga-losa.
Según el programa, la máxima flecha de la viga en este caso es de 18 [mm].
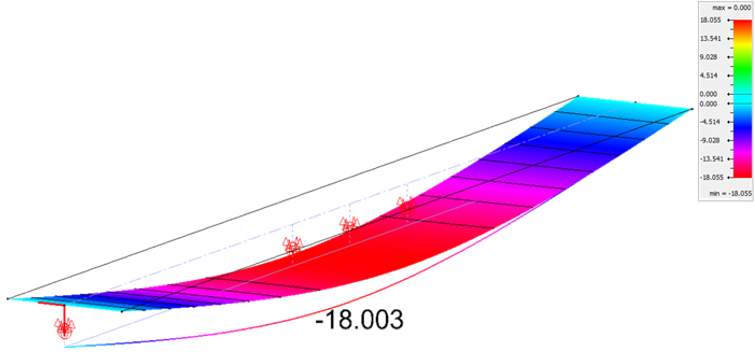
Figura 9. Deformación caso sin interacción.
RESULTADO TEÓRICO
La deflexión de una viga simplemente apoyada se puede determinar integrando la ley de momentos de la siguiente manera:
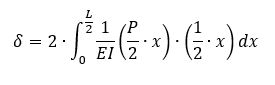
Los porcentajes de carga que absorbe la viga de acero y la losa de hormigón dependen de sus respectivas rigideces y se pueden determinar igualando las deformaciones de ambos elementos:
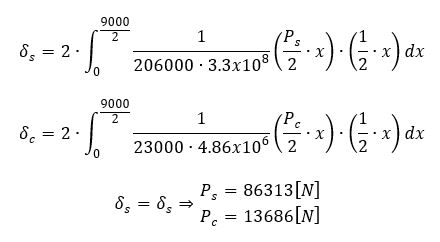
Sabiendo la carga que absorbe la viga de acero se puede determinar la deflexión de esta (que es la misma que la del conjunto) de la siguiente forma:
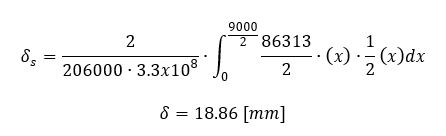
CASO 2: INTERACCIÓN COMPLETA
RESULTADO EN DIAMONDS
Para modelizar este caso, simplemente se definen ambos elementos y al igual que en el caso 1, se debe especificar que la cara superior de la viga coincida con la cara inferior de la losa.
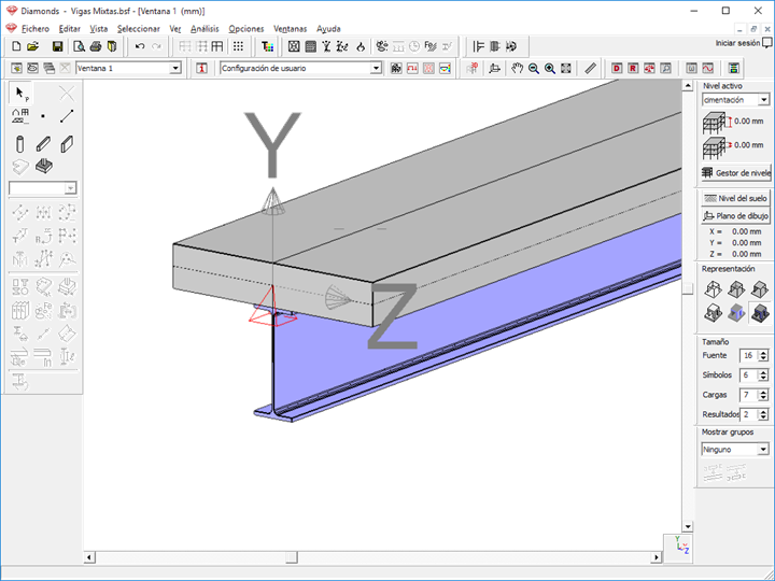
Figura 10. Modelo Diamonds Caso 2.
En este caso, Diamonds automáticamente considerará que ambos elementos trabajan solidariamente.
*Nota: Otra forma de modelar este caso consiste en definir la sección mixta usando el editor de secciones personalizadas del programa (Ver Figura 11). De todas formas, con cualquiera de los dos métodos se obtienen los mismos resultados.
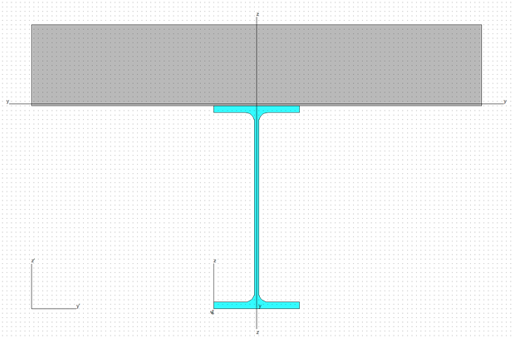
Figura 11. Sección mixta modelada en el editor de secciones personalizadas.
Según el programa, la máxima flecha de la viga en este caso es de 6.59 [mm].
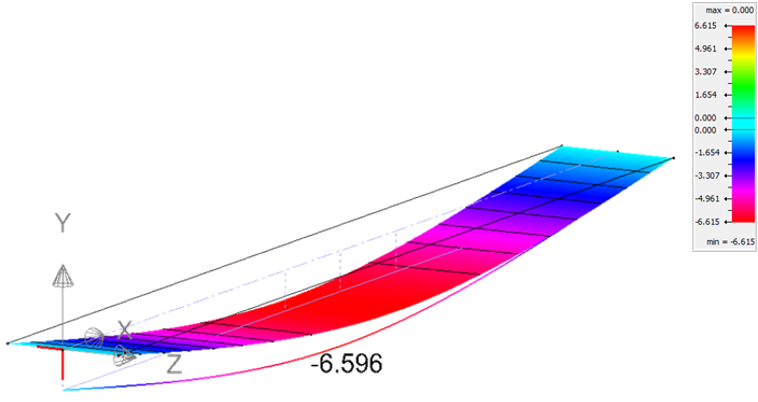
Figura 12. Deformación caso con Interacción perfecta.
RESULTADO TEÓRICO
En este caso se debe trabajar con la inercia de la sección mixta. Para obtener esta inercia se debe trabajar la losa de hormigón como una pieza de acero con dimensiones equivalentes. Esto se logra dividiendo el ancho de la losa por el coeficiente de equivalencia n (Es/Ec).
La flecha obtenida con las propiedades equivalentes de la sección mixta se muestra a continuación:
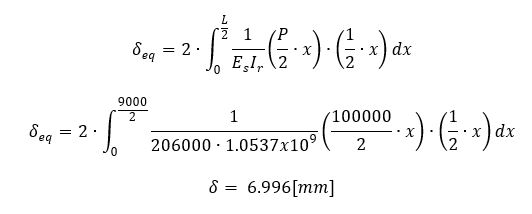
El resultado coincide aproximadamente con el obtenido por el programa.
CASO 3: INTERACCIÓN PARCIAL
RESULTADO EN DIAMONDS
En este caso se supondrá que la conexión se hace con pernos dúctiles de y de de largo. El número de pernos considerados será la mitad de los necesarios para la conexión perfecta.
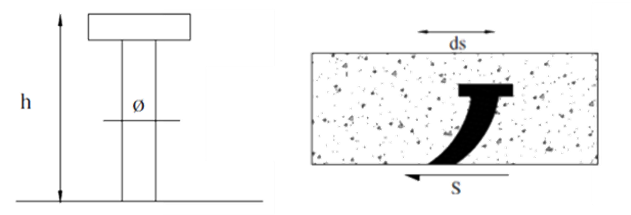
Figura 13. Pernos dúctiles supuestos para la conexión.
Número de pernos para conexión perfecta:
El esfuerzo rasante máximo en estado límite último considerando conexión perfecta es el siguiente:

La capacidad resistente de los pernos considerados es de que corresponden a la rotura del hormigón circundante al perno. Por lo tanto, el número de conectores para conexión perfecta es:
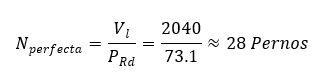
Número de pernos considerados para conexión imperfecta:
Como en este caso se busca interacción imperfecta, se considerará un número de pernos igual a la mitad de los calculados para interacción perfecta.

Para modelizar este caso en Diamonds, se define la viga y la losa y se conectan mediante elementos de tipo “enlace rígido” para representar los pernos conectores.
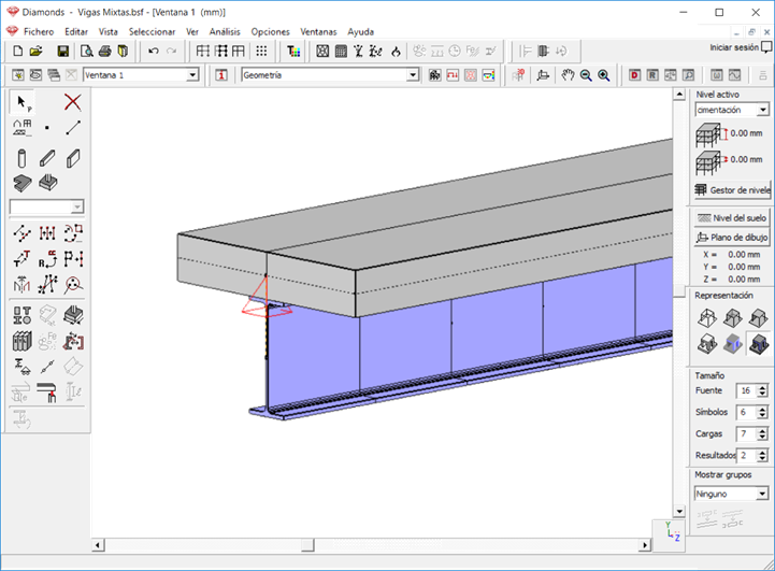
Figura 14. Modelo Diamonds Caso 3.
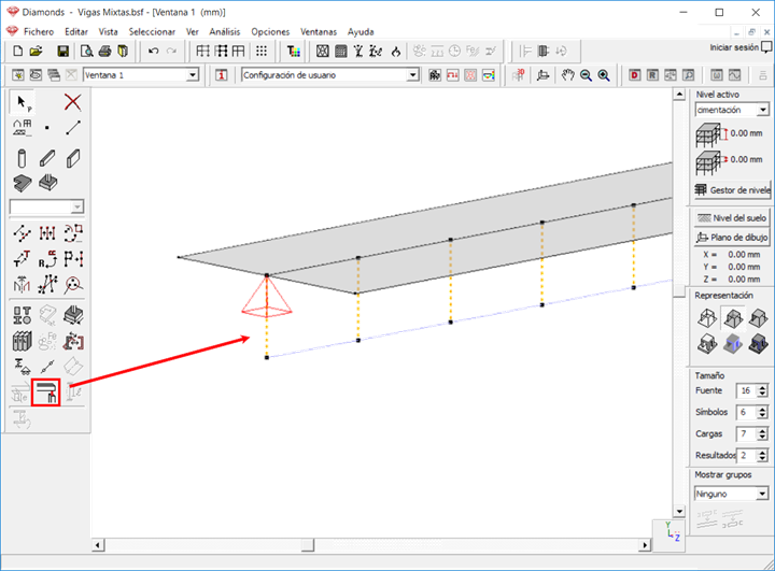
Figura 15. Definición de enlaces rígidos.
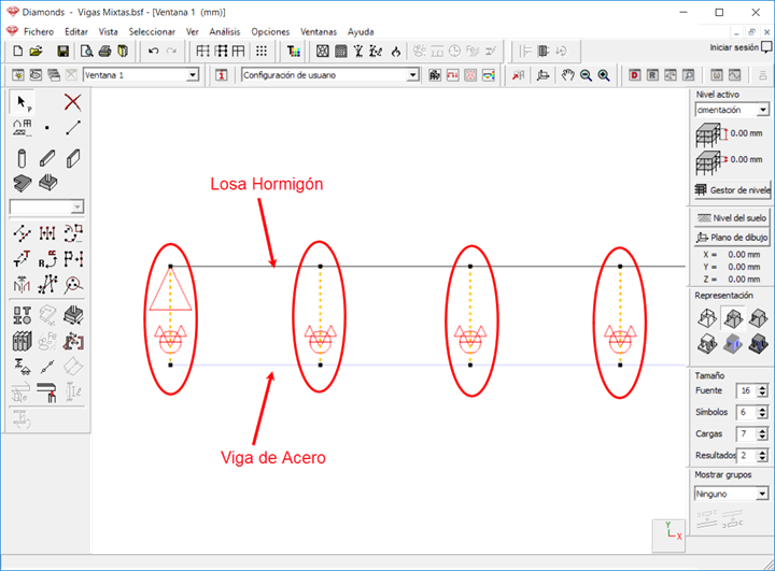
Figura 16. Pernos modelados como enlaces rígidos con esfuerzo rasante restringido.
A estos enlaces rígidos, se les libera la transmisión de momento. Mientras que la trasmisión de cortante se aproxima mediante una función que represente la curva de rigidez de los pernos.
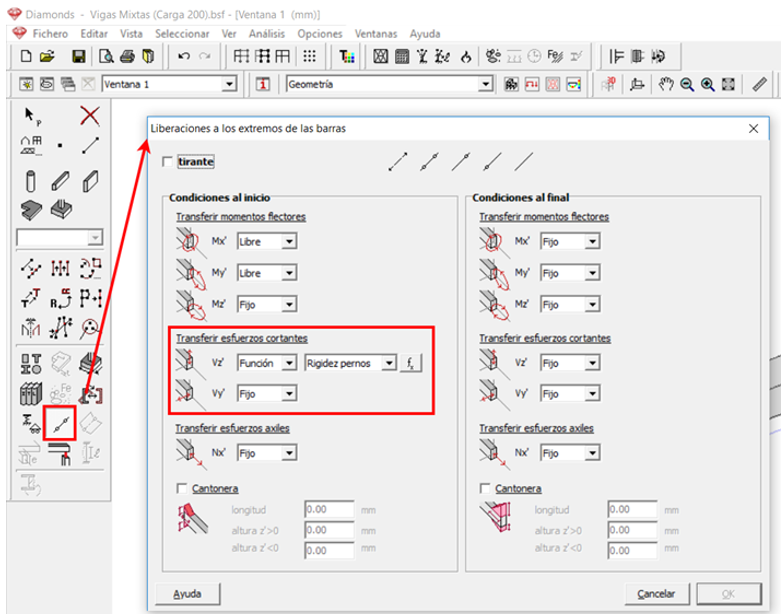
Figura 17. Transferencia de esfuerzo rasante.
Dado que los conectores son dúctiles, tendrán un comportamiento elasto-plástico como el que se muestra en la Figura 18. En Diamonds se usará una curva bilineal (pero de igual forma, se podría hacer una curva más aproximada al caso real).
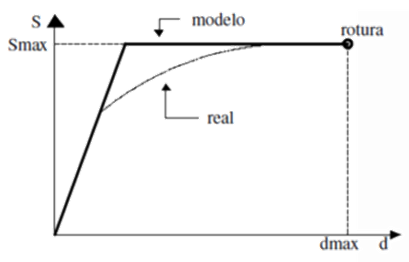
Figura 18. Curva de rigidez de los pernos dúctiles considerados.
La función utilizada es la siguiente:
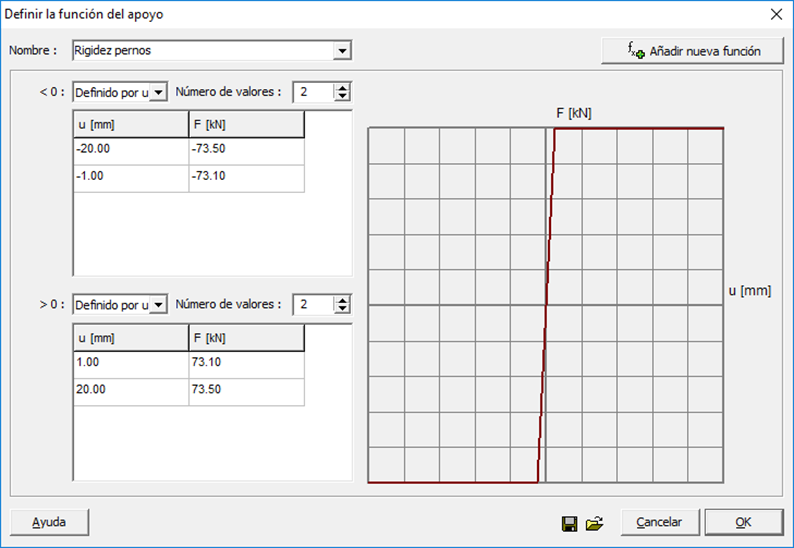
Figura 19. Función de transferencia de esfuerzo rasante.
Según el programa, la máxima flecha de la viga en este caso es de 9.30 [mm].
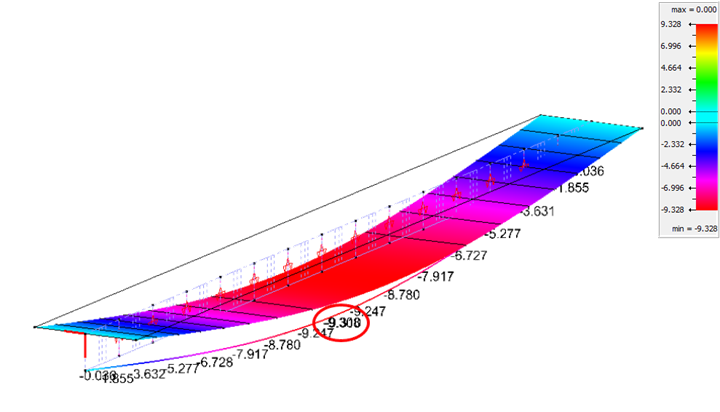
Figura 20. Deformación caso con Interacción imperfecta.
RESULTADO TEÓRICO
El máximo momento resistente de la sección critica de una viga mixta con conexión imperfecta, se puede estimar aproximadamente, con una interpolación lineal entre los casos de interacción nula e interacción perfecta (EN 1994_1_1). La Figura 21, muestra la relación entre número de conectores y momento resistente de la sección crítica.
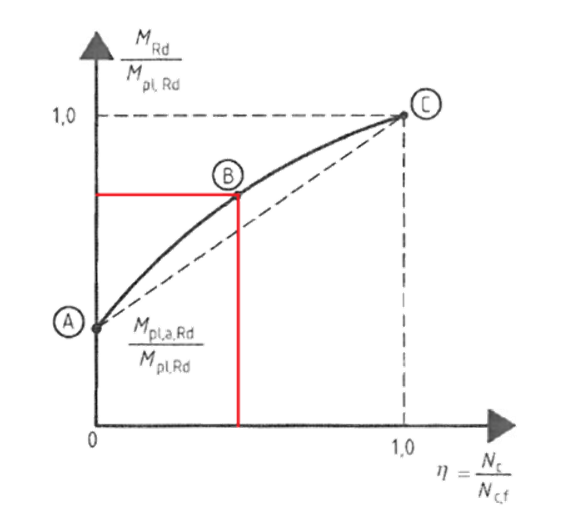
Figura 21. Relación entre número de conectores y momento resistente.
De la Figura anterior se desprende que para un número de conectores igual a la mitad de los conectores necesarios para interacción perfecta (n=0.5), el momento último será aproximadamente la mitad entre el momento último asociado a la conexión perfecta y el momento último de la viga de acero.
Si bien la viga estudiada no está sometida a un momento cercano al último, se puede suponer que la redistribución plástica de cortante a través de los conectores hará que el momento en la sección crítica de la viga disminuya proporcionalmente al grado de conexión de la unión (n). Observar que el momento real, será mayor al obtenido haciendo interpolación lineal, por lo tanto, la deformada calculada interpolando será un límite superior para la deformación real de la viga mixta.

Como se comentó anteriormente este resultado es una aproximación del límite superior de la deformación con conectores dúctiles. Se puede ver que efectivamente este valor es ligeramente superior al obtenido en Diamonds (9.3 [mm]).
Así es como se modelizan vigas de acero con losas de hormigón. Si te interesa información sobre el Curso Cálculo de Estructuras con Diamonds, contacta con nosotros.
