Rigidez de placas en Diamonds 2019

 

La palabra ‘placa’ es un término colectivo para aquellos elementos en los que las cargas pueden transferirse en dos direcciones. Forjados, muros, losas y contrachapados, todos ellos pueden considerarse placas.

 

Figura 0.1. Ejemplos de placas.

 

Las placas pueden cargarse en su plano, o perpendiculares a su plano. El comportamiento de membrana describe cómo una placa resiste las cargas en su plano. El comportamiento a flexión describe como una placa resiste las cargas perpendiculares a su plano.

Para describir dichos comportamientos se necesita conocer la rigidez de la placa. La rigidez es una medida de la resistencia de un elemento contra la deformación.

Una vez la rigidez es conocida, Diamonds la utilizará en su Método de elementos finitos (o FEM: Finite Element Method). El FEM divide la estructura en un número finito de elementos, que serán conectados de forma coherente unos a otros, permitiendo al software calcular los desplazamientos de la estructura. Las tensiones (y los esfuerzos resultantes) pueden deducirse de los desplazamientos por estas relaciones entre ellos:

• Las ecuaciones cinemáticas dan las relaciones entre los desplazamientos y las deformaciones.
• Las ecuaciones constitutivas dan información del comportamiento del material, a la vez que proveen relaciones entre las tensiones y las deformaciones.
• Las ecuaciones de equilibrio dan relaciones entre las cargas y las tensiones.

Con el objetivo de determinar la rigidez en las placas, el estudio se centrará en la ecuación constitutiva.

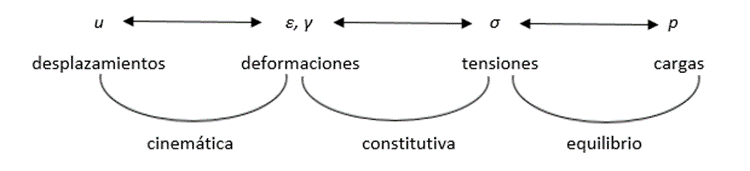
Figura 0.2. Esquema de relaciones en una placa.

 

PLACA ISOTRÓPICA

La forma más simple para una placa es una placa isotrópica. La palabra ‘isotrópica’ se refiere al comportamiento del material y significa ‘homogéneo en todas las direcciones’, como el acero sólido. La primera parte de este apartado describe la relación entre la tensión y la deformación para un material isotrópico para que los esfuerzos en la sección (fuerzas de membrana y/o fuerzas de flexión) puedan calcularse en la segunda parte de este apartado. La tercera parte de este apartado consiste en un ejemplo que muestra cómo aplicar estos conceptos.

ECUACIONES CONSTITUTIVAS

LEY DE HOOKE EN 3D

Si el material está sujeto a un estado de fuerza triaxial, se desarrollarán deformaciones normales en el material. La deformación total en una dirección equivale a la suma de todas las deformaciones en aquella dirección debidas a las tensiones en cada dirección [4]:

 

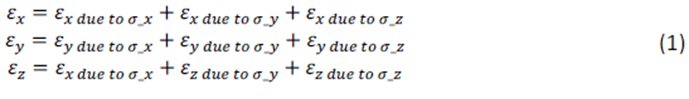
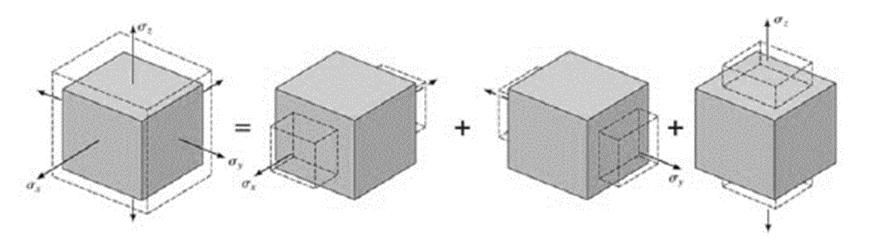
Figura 0.3. Ley de Hooke para tensión axil.

 

Tomando la ley de Hooke (σ =E · ε ) y el coeficiente de Poisson , las expresiones en (1) se transforman en:

 

 

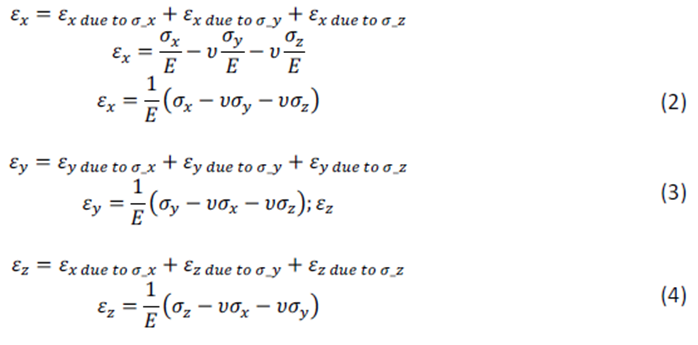
Si se aplica una fuerza cortante Txy al elemento, el material se modificará únicamente a causa de una deformación cortante Yxy; eso significa que la tensión Txy no causará otras deformaciones en el material. De la misma forma, Tyz y Txz solo causarán deformaciones cortantes Yyz y Yxz.

 

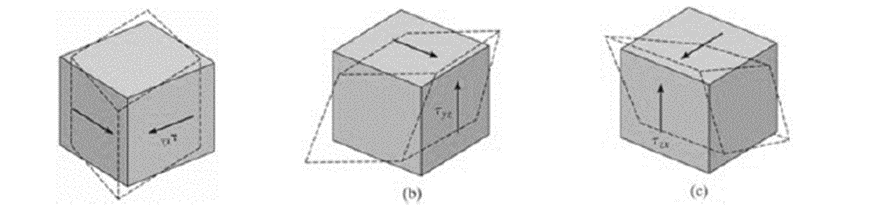
Figura 0.4. Ley de Hooke para tensión cortante.

 

La ley de Hooke que relaciona la tensión y la deformación cortante es:

 

 

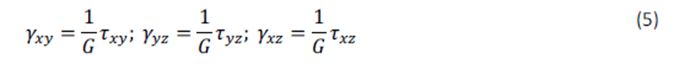
Escribiendo las ecuaciones (2), (3), (4) y (5) en forma matricial (tensión-deformación) se obtiene la ley de Hooke para un material lineal elástico en 3D:

 

 

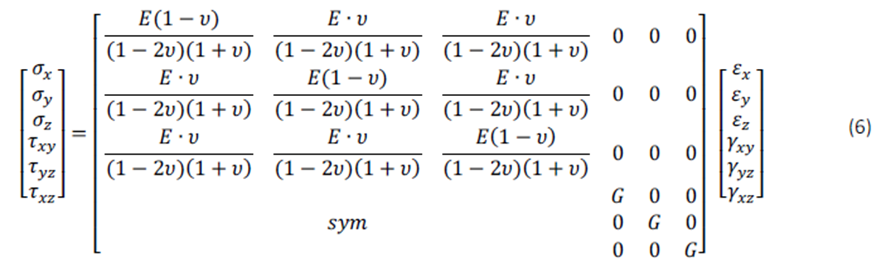
LEY DE HOOKE EN 2D

Si la placa es delgada y no existen cargas fuera del plano, puede considerarse quedar sometida únicamente a cargas en el plano. Así, σy = 0, Txz = 0. La ecuación (6) queda de la siguiente forma:

 

 

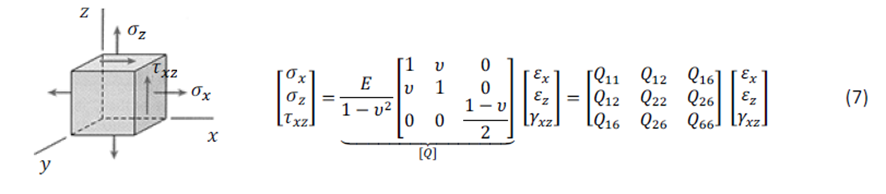
La matriz 3×3 [Q] en la ecuación (7) recibe el nombre de matriz elástica.

Nota: Una forma alternativa de transformar la ley de Hooke en 3D a 2D es la deformación en el plano. Pero como Diamonds trabaja con tensión en el plano, esto no se tratará.

 

ESFUERZOS RESULTANTES

Las fuerzas de membrana resultantes y los momentos pueden calcularse integrando las tensiones (eq. (7)) tomando el espesor t de la placa:

 

 

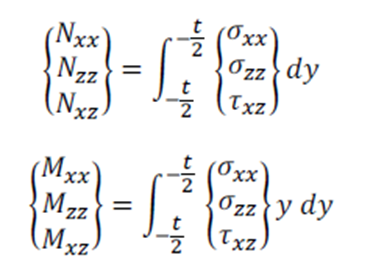
Esto resulta en la siguiente matriz de ecuaciones (donde ni σxx ni ε dependen del espesor):

 

 

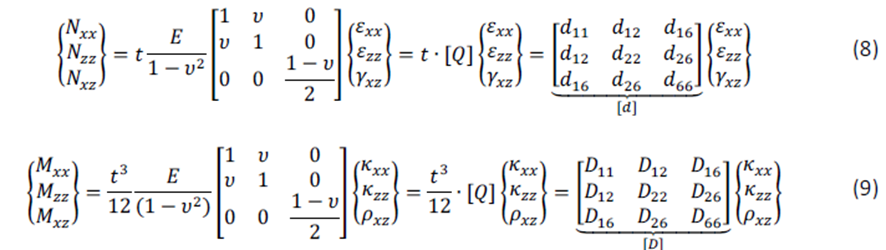
La ecuación (8) expresa el comportamiento de membrana de una placa isotrópica, la ecuación (9), el comportamiento a flexión.

Notas:

• La matriz 3×3 en la ecuación (8) es llamada matriz de rigidez de membrana de la placa.
• En Diamonds, las ecuaciones (8) y (9) se trabajan en una ecuación matricial (10). Además, se considera d16 = d26 = D16 = D26 =0 (esto se comenta en el apartado Otros tipos de placa):

 

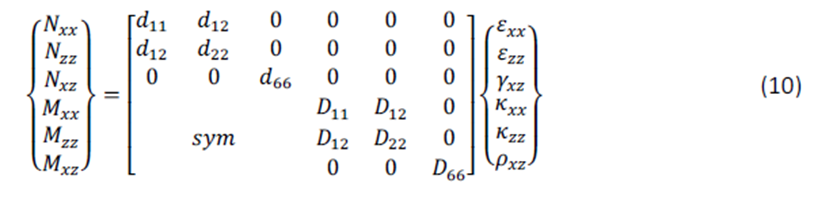
EJEMPLO: GEOMETRÍA ISOTRÓPICA – MATERIAL ISOTRÓPICO

 

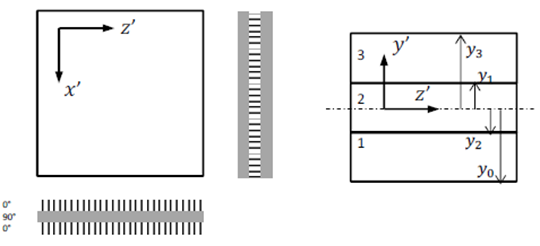
Figura 0.5. Ejemplo placa isotrópica.

 

CÁLCULO MANUAL

Se utiliza la ecuación (8) para describir el comportamiento de membrana.

 

 

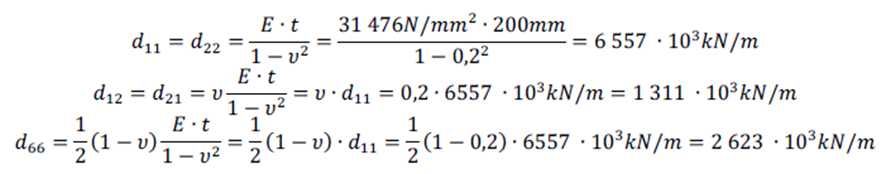
Se utiliza la ecuación (9) para describir el comportamiento a flexión.

 

 

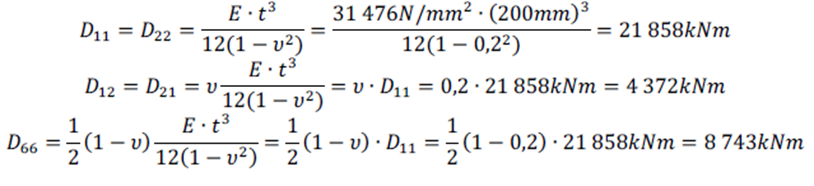
CÁLCULO EN DIAMONDS

La matriz de rigidez de una placa isotrópica en Diamonds da el mismo resultado que el calculado a mano:

 

Figura 0.6. Matriz placa isotópica en Diamonds.

 

Nota: Si desea compara la matriz de rigidez en Diamonds con cálculos manuales, asegúrese de que utiliza la norma correcta (en este caso, EN 1992-1-1 [–]). Algunos materiales tienen distintos módulos de Young dependiendo de la norma o el anejo nacional.

OTROS TIPOS DE PLACAS

Muchos tipos de placa no pueden tratarse como placas isotrópicas. Pueden existir rigidizadores y pueden ser distintos en las dos direcciones ortogonales (geometría ortótropa). No todos los materiales tienen propiedades isotrópicas, un material puede tener diferentes propiedades en dos direcciones perpendiculares. Este tipo de material es llamado ortótropo. Una placa también puede componerse de múltiples capas ortótropas. Este tipo de placa recibe el nombre de placa laminada.

A continuación, se presentan una serie de ejemplos de placas con las características anteriormente mencionadas.

 

GEOMETRÍA ORTÓTROPA – MATERIAL ISOTRÓPICO

 

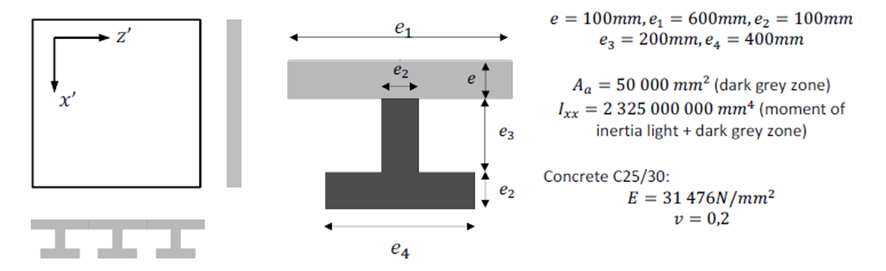
Figura 0.7. Ejemplo geometría ortótropa – material isotrópico.

 

En este ejemplo se reemplazará la forma real de la placa con una placa sólida teniendo en cuenta la geometría de los rigidizadores. Este método es llamado ortotropía de forma. Puede utilizarse para placas con repetidos rigidizadores con un espaciado regular.

Las fórmulas de los componentes de rigidez son [2]:

 

 

La rigidez torsional D66 merece una atención especial. Utilizar aquí la fórmula para una placa isotrópica infravalorará la rigidez torsional, porque se omiten los rigidizadores. La alternativa es calcular las rigideces torsionales por unidad de longitud en cada dirección (ixz y izx) y tomar la media, que resulta en D66,av. La fórmula para la rigidez por unidad de longitud se da en la Figura 0.8.

 

Figura 0.8. Rigidez torsional por unidad de longitud [2], [7].

 

CÁLCULO MANUAL

 

 

Para calcular la rigidez torsional en la dirección z (i12), la sección I puede verse como una suma de rectángulos [7]. En la dirección x’ (i21) se utiliza la fórmula para una placa isotrópica.

 

 

CÁLCULO EN DIAMONDS

Estos valores deberían introducirse manualmente en Diamonds.

 

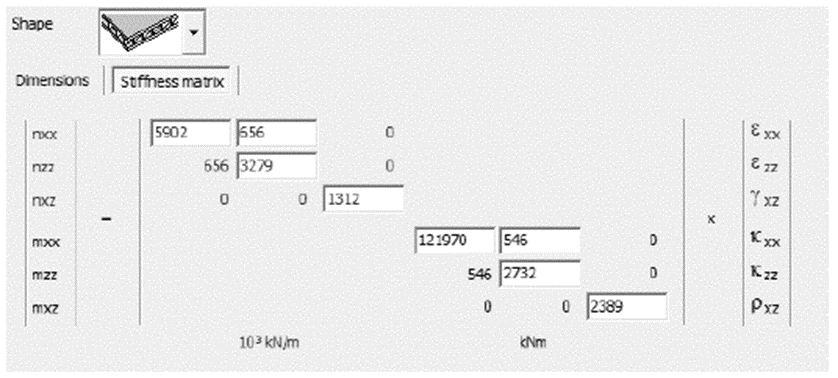
Figura 0.9. Matriz de rigidez definida por usuario en Diamonds.

 

Nota: Debido a que Diamonds no conoce la forma real de la placa, no pueden calcularse tensiones ni armaduras.

 

GEOMETRÍA ISOTRÓPICA – MATERIAL ORTÓTROPO

 

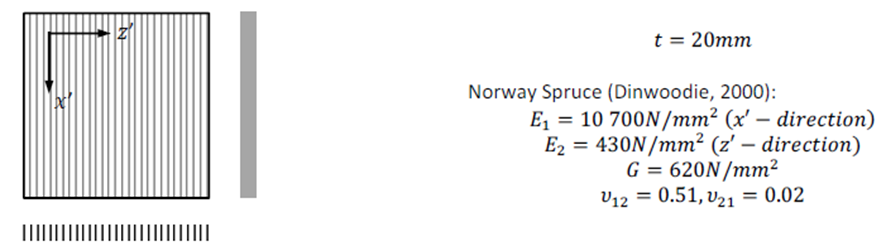
Figura 0.10. Ejemplo geometría isotrópica – material ortótropo.

 

Las fórmulas para los componentes de la rigidez son [5].

 

 

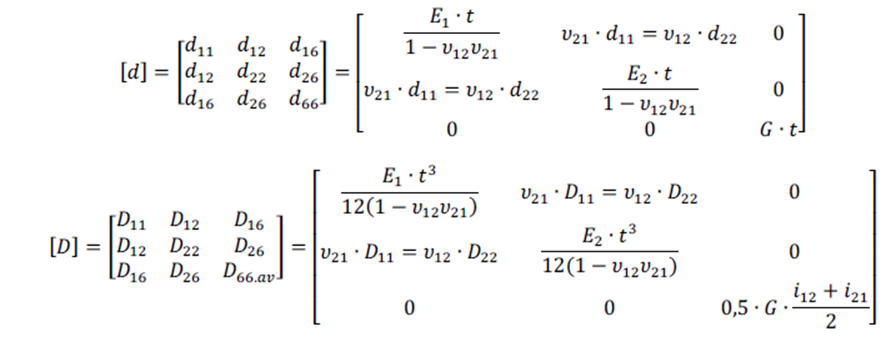
Se reconocen estas fórmulas para la matriz de elasticidad [Q]:

 

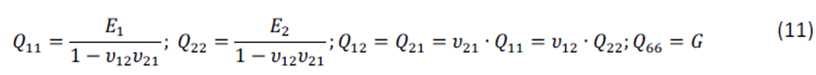
CÁLCULO MANUAL

 

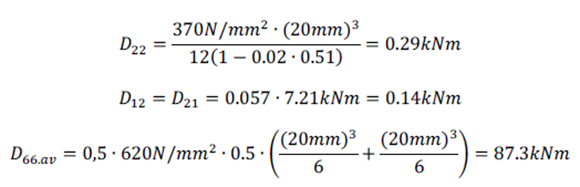
CÁLCULO EN DIAMONDS

Estos valores se deberían introducir en Diamonds manualmente.

 

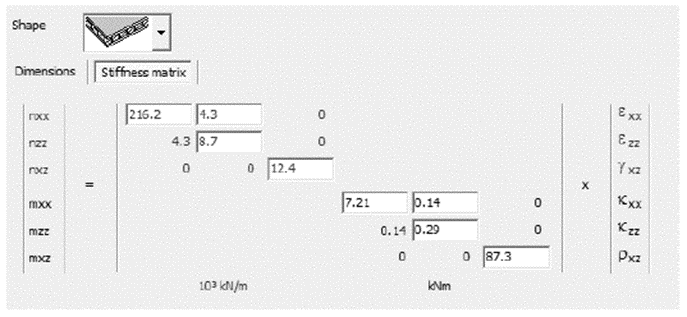
Figura 0.11. Matriz de rigidez definida por usuario en Diamonds.

 

Notas:

• Ya que Diamonds no conoce la forma real de la placa, no pueden calcularse tensiones ni armado en la placa.
• Si los ejes principales del sistema ortótropo se rotaran un ángulo 0 en relación con el sistema de coordenadas locales x´z´, la matriz de rigidez [Q] se transformaría en [Q]0. En la nueva matriz elástica [Q]0 los componentes [Q]16,0 y [Q]26,0 ya no son iguales a cero [6]. Diamonds asume [Q]16,0 = [Q]26 = 0, por lo que trabajar con una placa con los ejes principales rotados, no es posible en el software.

 

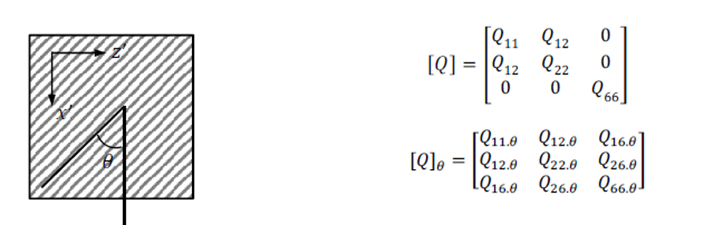
Figura 0.12. Componentes de matriz elástica rotada.

 

GEOMETRÍA ORTÓTROPA (LAMINADA) – MATERIAL ORTÓTROPO

 

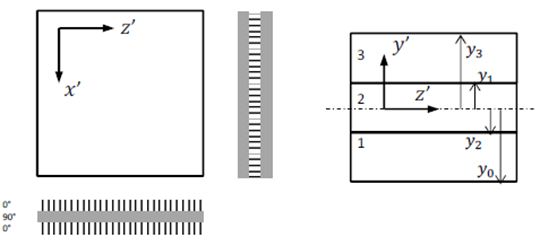
Figura 0.13. Ejemplo geometría ortótropa – material ortótropo.

 

Características de las 3 capas:

• Cada capa tiene un espesor de 20mm.
• Las capas se enumeran del 1 al 3 empezando por la inferior.

Para una placa laminada con múltiples capas, la relación para los esfuerzos resultantes es un poco más compleja que la comentada en el apartado Placa isotrópica. El propósito es tomar la suma de las contribuciones de todas las capas laminadas k  [2] (Kubiak, 2013).

 

 

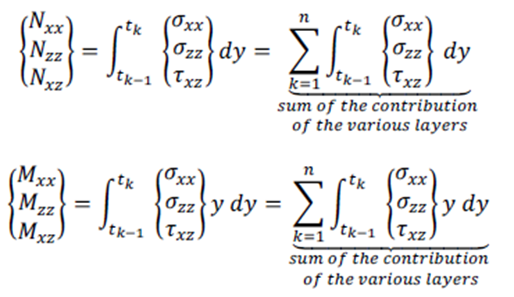
*Suma de las contribuciones de las distintas capas.

Resultando en estas ecuaciones matriciales:

 

 

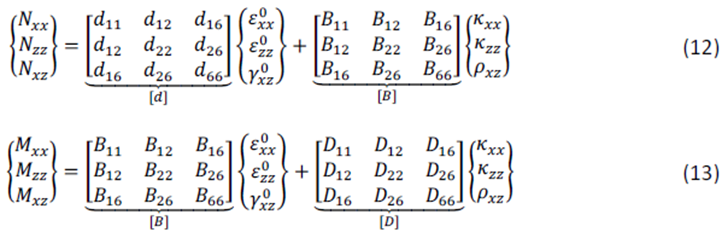
Los componentes en la matriz [d], [B] y [D] se calculan con la fórmula:

 

 

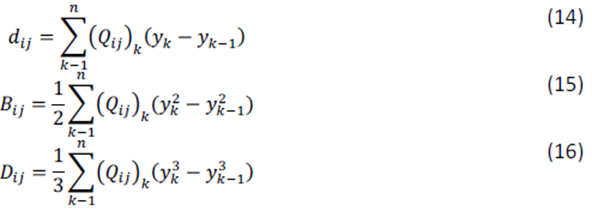
Las matrices 3×3 [d] y [D] en las ecuaciones (12) y (13) son, de nuevo, las matrices de rigidez de membrana y de flexión. Formalmente la matriz [d] es nombrada como [A]. La matriz 3×3 [B] de las ecuaciones (12) y (13) es llamada matriz de acoplamiento y relaciona las fuerzas en el plano y las deformaciones fuera del plano. Qij es el componente relevante de la matriz de rigidez en las ecuaciones (14), (15) y (16). “y” es la distancia desde el borde más extremo de una capa al centro del plano.

 

CÁLCULO MANUAL

La matriz de elasticidad para una capa a 0º es (11):

 

 

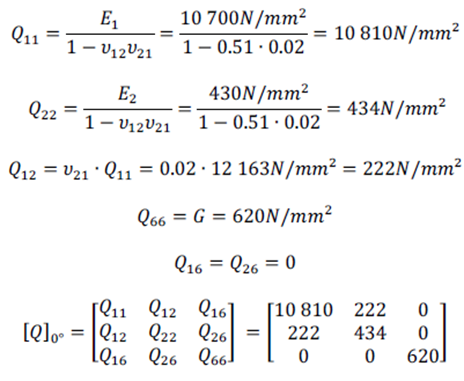
En la matriz de elasticidad para una capa a 90°, Q11  y  Q22 se han intercambiado la posición debido a que la dirección principal ha rotado 90º.

 

 

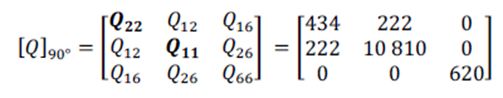
El primer componente  d11 de la rigidez de membrana se calcula con la ecuación (14):

 

 

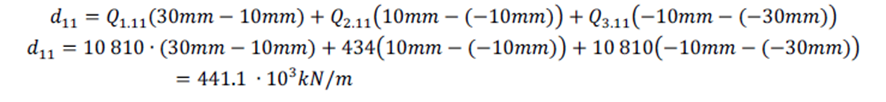
El resto de las componentes pueden encontrarse de la misma forma:

 

 

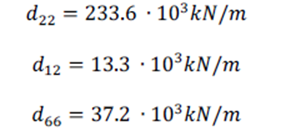
El primer componente D11 de la rigidez de membrana se calcula con la ecuación (16):

 

 

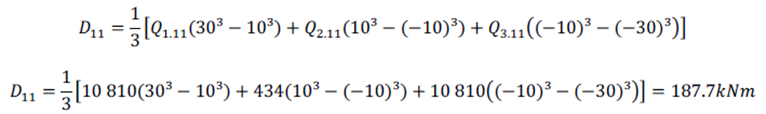
El resto de los componentes pueden hallarse de la misma forma:

 

 

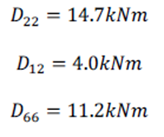
CÁLCULO EN DIAMONDS

Estos valores deberían introducirse manualmente en Diamonds.

 

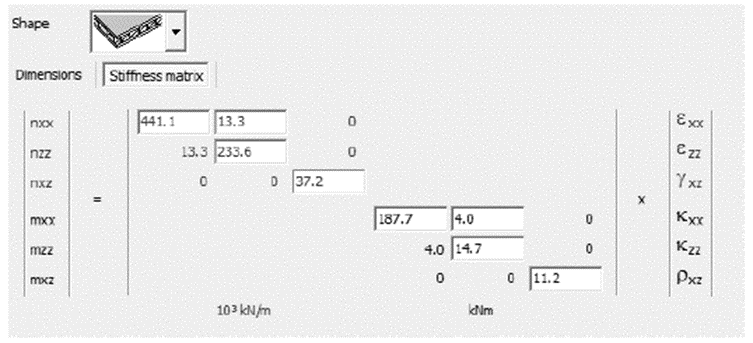
Figura 0.14. Matriz de rigidez definida por usuario en Diamonds.

 

Notas:

• Dado que la forma real de la placa no es conocida por Diamonds, no pueden calcularse tensiones ni armados.
• Debe prestarse atención cuando se calculen las tensiones: La deformación varía linealmente a través de las capas. No obstante, las propiedades de la rigidez (y por tanto también las tensiones) son discontinuas de una capa a la siguiente.

 

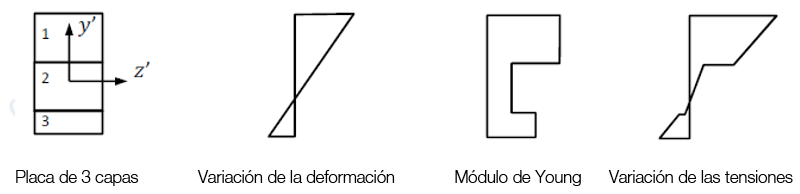
Figura 0.15. Variación de la tensión y la deformación en una placa laminada de 3 capas (hipotética).

 

• La matriz de rigidez en Diamonds asume [1]:
  • D16 = d26 = 0
  • D16 = D26 = 0
  • [B] = 0

Esto será cierto si todas las capas están orientadas a 0° o 90° y cuando la composición de las capas sea simétrica.

 

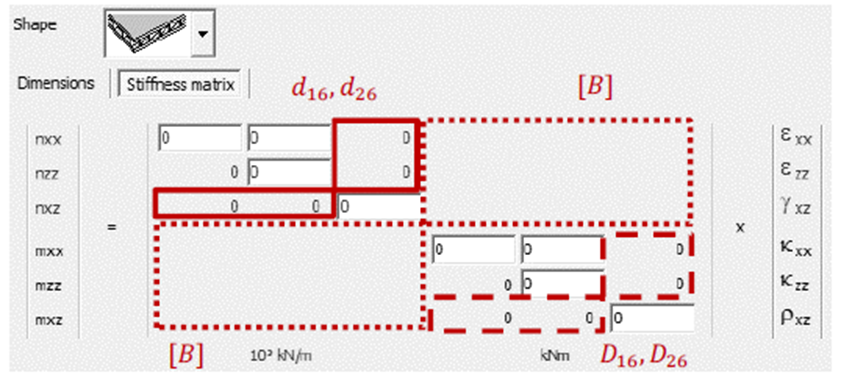
• Los valores calculados pueden verificarse con la herramienta de la web de eFunda: http://www.efunda.com/formulae/solid_mechanics/composites/calc_ufrp_abd_go.cfm

Figura 0.16. Componentes considerados nulos por Diamonds.